点
点(point)是空间中的一个位置,没有大小、宽度。
在四维的齐次坐标里面,点的w分量设为1,如此,使用$4×4$矩阵对一个点进行变换时,平移、旋转、缩放都会施加于该点。
矢量
矢量(vector)也被称为向量,是空间中一个包含了模(矢量的长度)和方向(矢量在空间中的指向)的有向线段,没有位置。
在四维的齐次坐标里面,矢量的w分量设为0,如果,使用$4×4$矩阵对矢量进行变换时,平移的效果会被忽略,因为矢量是没有位置的。
矢量和标量的乘
$$k\mathbf{v}=(kv_x,kv_y,kv_z)$$
矢量和标量的除
$$\dfrac{\mathbf{v}}{k}=\dfrac{(v_x,v_y,v_z)}{k}=\dfrac{1}{k}(v_x,v_y,v_z)=({\dfrac{v_x}{k},\dfrac{v_y}{k},\dfrac{v_z}{k}})$$
矢量加法
$$\mathbf{a}+\mathbf{b}=(a_x+b_x,a_y+b_y,a_z+b_z)$$
矢量减法
$$\mathbf{a}-\mathbf{b}=(a_x-b_x,a_y-b_y,a_z-b_z)$$
矢量的模
$$|\mathbf{v}|=\sqrt{v_x^2+v_y^2+v_z^2}$$
矢量的归一化
$$_{\Large {\mathbf{v}}}^{∧}=\dfrac{\mathbf{v}}{|\mathbf{v}|}$$
矢量的点积(内积)
$$\mathbf{a}·\mathbf{b}=\mathbf{b}·\mathbf{a}=|\mathbf{a}||\mathbf{b}|cosθ=(a_x,a_y,a_z)·(b_x,b_y,b_z)=a_xb_x+a_yb_y+a_zb_z$$
$${\Large{\mathbf{a}}}^{∧}·{\Large{\mathbf{c}}}^{∧}=\dfrac{直角边}{斜边}=cosθ$$
数学意义
- 用于判断2个矢量的朝向
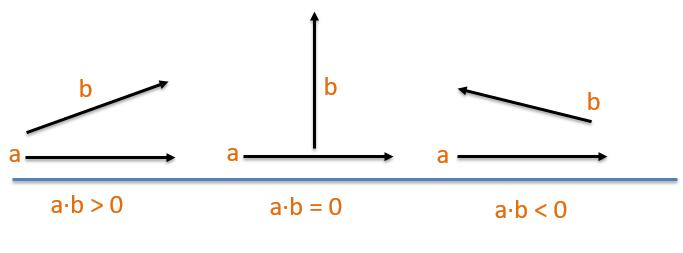
矢量的叉积(外积)
$$\mathbf{a}×\mathbf{b}=(a_x,a_y,a_z)×(b_x,b_y,b_z)=(a_yb_z-a_zb_y, a_zb_x-a_xb_z,a_xb_y-a_yb_x)$$
$$\mathbf{a}×\mathbf{b}≠\mathbf{b}×\mathbf{a}$$
$$\mathbf{a}×\mathbf{b}=-(\mathbf{b}×\mathbf{a})$$
$$(\mathbf{a}×\mathbf{b})×\mathbf{c}≠\mathbf{a}×(\mathbf{b}×\mathbf{c})$$
$$|\mathbf{a}×\mathbf{b}|=|\mathbf{a}||\mathbf{b}|sinθ$$
数学意义
- 用于求平面的法向量
矩阵
矩阵和标量相乘
$$kM=Mk=k\left[\begin{matrix}m_{11} & m_{12} & m_{13} \m_{21} & m_{22} & m_{23} \m_{31} & m_{32} & m_{33}\end{matrix}\right]=\left[\begin{matrix}km_{11} & km_{12} & km_{13} \km_{21} & km_{22} & km_{23} \km_{31} & km_{32} & km_{33}\end{matrix}\right]$$
矩阵和矩阵相乘
$$A_{r×n}B_{n×c}=C_{r×c}$$
$$c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+…+a_{in}b_{nj}=\sum_{k=1}^{n}{a_{ik}b_{kj}}$$
$$AB≠BA$$
$$(AB)C=A(BC)$$
例子
$$A_{4×2}B_{2×4}=C_{4×4}\left[\begin{matrix}a_{11} & a_{12} \a_{21} & a_{22} \a_{31} & a_{32} \a_{41} & a_{42}\end{matrix}\right]\left[\begin{matrix}b_{11} & b_{12} & b_{13} & b_{14}\b_{21}& b_{22} & b_{23} & b_{24}\end{matrix}\right]=\left[\begin{matrix}c_{11} & c_{12} & c_{13} & c_{14}\c_{21}& c_{22} & c_{23} & c_{24} \ c_{31} & c_{32} & c_{33} & c_{34}\c_{41} & c_{42} & c_{43} & c_{44}\end{matrix}\right]$$
$$c_{23}=a_{21}b_{13}+a_{22}b_{23}$$
方块矩阵
行和列数量相对的矩阵,加方块矩阵
$$\left[\begin{matrix}a_{11} & a_{12} & a_{13} & a_{14}\a_{21}& a_{22} & a_{23} & a_{24} \ a_{31} & a_{32} & a_{33} & a_{34}\a_{41} & a_{42} & a_{43} & a_{44}\end{matrix}\right]$$
对角矩阵
除了对角元素都为0的方块矩阵,叫对角矩阵
$$\left[\begin{matrix}a_{11} & 0 & 0 & 0\0& a_{22} & 0 & 0 \ 0 & 0 & a_{33} & 0\0 & 0 &0 & a_{44}\end{matrix}\right]$$
单位矩阵
对角都为1,其它元素为0的方块矩阵,叫单位矩阵
$$\left[\begin{matrix}1 & 0 & 0 & 0\0&1 & 0 & 0 \ 0 & 0 & 1 & 0\0 & 0 &0 & 1\end{matrix}\right]$$
性质
- 单位矩阵与任何矩阵相乘得到的矩阵都是原来的矩阵。
$$MI=IM=M$$
转置矩阵
把原矩阵行列翻转得到的矩阵就是转置矩阵
$$M_{ij}^T=M_{ji}$$
$$\left[\begin{matrix}x & y & z\end{matrix}\right]^T=\left[\begin{matrix}x \ y \ z\end{matrix}\right]$$
$$\left[\begin{matrix}x \ y \ z\end{matrix}\right]^T=\left[\begin{matrix}x & y & z\end{matrix}\right]$$
性质
- 转置矩阵的转置等于原矩阵
$$(M^T)^T=M$$
- 矩阵串接的转置等于反向串接各个矩阵的转置
$$(AB)^T=B^TA^T$$
逆矩阵
不是所有的矩阵都有逆矩阵,逆矩阵的出现必现满足一定条件:矩阵要是方块矩阵,矩阵的行列式不为0
性质
- 矩阵与其逆矩阵相乘结果为单位矩阵
$$MM^{-1}=M^{-1}M=I$$
- 逆矩阵的逆矩阵是原矩阵本身
$$(M^{-1})^{-1}=M$$
- 转置矩阵的逆矩阵是逆矩阵的转置
$$(M^T)^{-1}=(M^{-1})^T$$
- 矩阵串接相乘后的逆矩阵等于反向串接各个矩阵的逆矩阵
$$(AB)^{-1}=B^{-1}A^{-1}$$
数学意义
- 对变换进行还原
我们使用了变换矩阵$M$对矢量$v$进行了一次变换得到了$w$,要还原$w$为$v$,我们可以通过使用$M^{-1}$与$w$进行变换就可以还原得到原来矢量
$$Mv=w$$
$$M^{-1}w=v$$
正交矩阵
如果一个方阵和它的转置矩阵的乘积是单位矩阵,那么这个方阵就是正交矩阵
$$MM^{T}=M^{T}M=I$$
$$MM^T=\left[\begin{matrix}- & m_1 & - \-& m_2 & - \ - & m_3 & -\\end{matrix}\right]\left[\begin{matrix}| & | & | \m_1& m_2 & m_3 \ | & | & |\\end{matrix}\right]=\left[\begin{matrix}m_1·m_1 & m_1·m_2 & m_1·m_3 \m_2·m_1& m_2·m_2 & m_2·m_3 \ m_3·m_1 & m_3·m_2 & m_3·m_3\\end{matrix}\right]=\left[\begin{matrix}1 & 0 & 0 \0&1 & 0 \ 0 & 0 & 1\\end{matrix}\right]=I$$
数学要求
$$\left[\begin{matrix}m_1·m_1=1 & m_1·m_2=0 & m_1·m_3=0 \m_2·m_1=0& m_2·m_2=1 & m_2·m_3=0 \ m_3·m_1=0 & m_3·m_2=0 & m_3·m_3=1\\end{matrix}\right]=\left[\begin{matrix}1 & 0 & 0 \0&1 & 0 \ 0 & 0 & 1\\end{matrix}\right]=I$$
- 矩阵的每一行,即$m_1$,$m_2$,$m_3$都必须是单位矢量,这样它们与自己的点积才能是1
- 矩阵的每一行,即$m_1$,$m_2$,$m_3$各矢量相互垂直,这样它们自己的点积才能是0
性质
- 正交矩阵的转置矩阵就是逆矩阵
$$M^{T}=M^{-1}$$
变换
我们把点、方向矢量等数据通过某种方式进行转换的过程称为变换。
- 常见变换
| 变换名称 | 线性变换 | 仿射变换 | 可逆矩阵 | 正交矩阵 |
|---|---|---|---|---|
| 平移矩阵 | × | √ | √ | × |
| 绕坐标轴旋转的旋转矩阵 | √ | √ | √ | √ |
| 绕任意轴旋转的旋转矩阵 | √ | √ | √ | √ |
| 按坐标轴缩放的缩放矩阵 | √ | √ | √ | × |
| 错切矩阵 | √ | √ | √ | × |
| 镜像矩阵 | √ | √ | √ | √ |
| 正交投影矩阵 | √ | √ | × | × |
| 透视投影矩阵 | × | × | × | × |
线性变换
线性变换指的是那些可以保留矢量加和标量乘的变换。
$$f(x)+f(y)=f(x+y)$$
$$kf(x)=f(kx)$$
仿射变换
仿射变换是合并线性变换和平移变换的变换类型,可以使用$4×4$矩阵来表示。
平移
- 平移矩阵:
$$M_{translation}=\left[\begin{matrix}1 & 0 & 0 & p_x \0 & 1 & 0 & p_y \0 & 0 & 1 & p_z \0 & 0 & 0 & 1\end{matrix}\right]$$
- 平移矩阵逆矩阵:
$$M_{translation}^{-1}=\left[\begin{matrix}1 & 0 & 0 & -p_x \0 & 1 & 0 & -p_y \0 & 0 & 1 & -p_z \0 & 0 & 0 & 1\end{matrix}\right]$$
- 点平移公式:
$$p_{result}=M_{translation} × p_{old}=\left[\begin{matrix}1 & 0 & 0 & p_x \0 & 1 & 0 & p_y \0 & 0 & 1 & p_z \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}x \y \z \1\end{matrix}\right]=\left[\begin{matrix}x+p_x \y+p_y \z+p_z \1\end{matrix}\right]$$
- 矢量平移公式:
$$v_{result}=M_{translation} × v_{old}=\left[\begin{matrix}1 & 0 & 0 & p_x \0 & 1 & 0 & p_y \0 & 0 & 1 & p_z \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}x \y \z \0\end{matrix}\right]=\left[\begin{matrix}x \y \z \0\end{matrix}\right]$$
缩放
- 缩放矩阵:
$$M_{scale}=\left[\begin{matrix}S_x & 0 & 0 & 0 \0 & S_y & 0 & 0 \0 & 0 & S_z & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
如果$S_x$=$S_y$=$S_z$,那么这个缩放就是统一缩放,否则是非统一缩放,统一缩放是扩大整个模型,不会改变角度和比例信息,而非统一缩放拉伸或挤压模型,会改变模型的角度和比例。
- 缩放矩阵逆矩阵:
$$M_{scale}^{-1}=\left[\begin{matrix}\dfrac{1}{S_x} & 0 & 0 & 0 \0 & \dfrac{1}{S_y} & 0 & 0 \0 & 0 & \dfrac{1}{S_z} & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
- 缩放公式:
$$v_{result}=M_{scale} × v_{scale}=\left[\begin{matrix}S_x & 0 & 0 & 0 \0 & S_y & 0 & 0 \0 & 0 & S_z & 0 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}x \y \z \1\end{matrix}\right]=\left[\begin{matrix}xp_x \yp_y \z*p_z \1\end{matrix}\right]$$
旋转
旋转矩阵是一个正交矩阵,即$M^T=M^{-1}$
- 绕x轴旋转矩阵:
$$M_{rotationX}=\left[\begin{matrix}1 & 0 & 0 & 0 \0 & cosθ & -sinθ & 0 \0 & sinθ & cosθ & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
- 绕y轴旋转矩阵:
$$M_{rotationY}=\left[\begin{matrix}cosθ & 0 & sinθ & 0 \0 & 1 & 0 & 0 \-sinθ & 0 & cosθ & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
- 绕z轴旋转矩阵:
$$M_{rotationZ}=\left[\begin{matrix}cosθ & -sinθ & 0 & 0 \sinθ & cosθ & 0 & 0 \0 & 0 & 1 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
- xyz旋转矩阵
$$M_{rotation} = M_{rotationY}M_{rotationX}M_{rotationZ}$$
阅读顺序从右到左,先进行z轴旋转,在进行x轴旋转,最后进行y轴旋转,反着(yxz)也可以。
变换组合
模型到世界
- 变换矩阵:
$$M_{m→w}=M_{translation}M_{rotation}M_{scale}$$
阅读顺序从右到左,先进行缩放变换,在进行旋转变换,最后进行平移变换。
- 坐标计算公式
$$p_{world}=M_{m→w}×p_{model}$$
例子
- 计算模型下某子节点在世界空间的坐标
父亲节点坐标(1,2,3),角度(30,60,90),缩放(4,5,6)
子节点在父亲节点内的坐标(-1,-2,-3)
$$p_{world}=M_{m→w}×p_{model}$$
$$M_{translation}=\left[\begin{matrix}1 & 0 & 0 & p_x \0 & 1 & 0 & p_y \0 & 0 & 1 & p_z \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}1 & 0 & 0 & 1 \0 & 1 & 0 & 2 \0 & 0 & 1 & 3 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{rotationX}=\left[\begin{matrix}1 & 0 & 0 & 0 \0 & cosθ & -sinθ & 0 \0 & sinθ & cosθ & 0 \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}1 & 0 & 0 & 0 \0 & 0.86603 & -0.5 & 0 \0 & 0.5 & 0.86603 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{rotationY}=\left[\begin{matrix}cosθ & 0 & sinθ & 0 \0 & 1 & 0 & 0 \-sinθ & 0 & cosθ & 0 \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}0.5 & 0 & 0.86603 & 0 \0 & 1 & 0 & 0 \-0.86603 & 0 & 0.5 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{rotationZ}=\left[\begin{matrix}cosθ & -sinθ & 0 & 0 \sinθ & cosθ & 0 & 0 \0 & 0 & 1 & 0 \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}0 & -1 & 0 & 0 \1 & 0 & 0 & 0 \0 & 0 & 1 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{scale}=\left[\begin{matrix}S_x & 0 & 0 & 0 \0 & S_y & 0 & 0 \0 & 0 & S_z & 0 \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}4 & 0 & 0 & 0 \0 & 5 & 0 & 0 \0 & 0 & 6 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{rotation}=M_{ry}M_{rx}m_{rz}=\left[\begin{matrix}0.5 & 0 & 0.86603 & 0 \0 & 1 & 0 & 0 \-0.86603 & 0 & 0.5 & 0 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}1 & 0 & 0 & 0 \0 & 0.86603 & -0.5 & 0 \0 & 0.5 & 0.86603 & 0 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}0 & -1 & 0 & 0 \1 & 0 & 0 & 0 \0 & 0 & 1 & 0 \0 & 0 & 0 & 1\end{matrix}\right]= \left[\begin{matrix}0.43301 & -0.5 & 0.75 & 0 \0.86603 & 0 &-0.5 & 0 \0.25 & 0.86603 & 0.43301 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{m→w}=M_{t}M_{r}M_{s}=\left[\begin{matrix}1 & 0 & 0 & 1 \0 & 1 & 0 & 2 \0 & 0 & 1 & 3 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}0.43301 & -0.5 & 0.75 & 0 \0.86603 & 0 &-0.5 & 0 \0.25 & 0.86603 & 0.43301 & 0 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}4 & 0 & 0 & 0 \0 & 5 & 0 & 0 \0 & 0 & 6 & 0 \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}1.73205 & -2.5 & 4.5 & 1 \3.46410 & 0 & -3 & 2 \1 & 4.33013 & 2.59808 & 3 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$p_{world}=M_{m→w}×p_{model}=\left[\begin{matrix}1.73205 & -2.5 & 4.5 & 1 \3.46410 & 0 & -3 & 2 \1 & 4.33013 & 2.59808 & 3 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}-1\-2 \-3 \1\end{matrix}\right]=\left[\begin{matrix}-9.232052\7.5359 \-14.45448 \1\end{matrix}\right]$$
计算是建议从右边开始,因为读法是如此,由于矩阵满足结合律所以从左边计算结果是一致。
$M_{ratation}=M_yM_xM_z=M_y(M_xM_z)$
$M_{m→w}=M_{t}M_{r}M_{s}=M_{t}(M_{r}M_{s})$
世界到观察
- 变换矩阵:
$$M_{w→v}=M_{scale}^{-1}M_{rotation}^{-1}M_{translation}^{-1}$$
阅读顺序从右到左,先进行平移还原,在进行旋转还原,最后进行缩放还原。
- 坐标计算公式
$$p_{view}=M_{w→v}×p_{world}$$
由于观察坐标的z轴与世界坐标的z轴是反的。所以计算出来的坐标的z需要取反
例子
- 计算模型在观察空间的坐标
模型世界坐标(1,2,3)
摄像机世界坐标(4,5,6),角度(90, 0, 0), 缩放(1, 1, 1)
$$M_{translation}=\left[\begin{matrix}1 & 0 & 0 & p_x \0 & 1 & 0 & p_y \0 & 0 & 1 & p_z \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}1 & 0 & 0 & 4 \0 & 1 & 0 & 5 \0 & 0 & 1 & 6 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{translation}^{-1}=\left[\begin{matrix}1 & 0 & 0 & -4 \0 & 1 & 0 & -5 \0 & 0 & 1 & -6 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{rotationX}=\left[\begin{matrix}1 & 0 & 0 & 0 \0 & cosθ & -sinθ & 0 \0 & sinθ & cosθ & 0 \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}1 & 0 & 0 & 0\0 & 0 & -1 & 0 \0 & 1 & 0 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{rotation}^{-1}=M_{rotationX}^{-1}=\left[\begin{matrix}1 & 0 & 0 & 0\0 & 0 & 1 & 0 \0 & -1 & 0 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{scale}=\left[\begin{matrix}s_x & 0 & 0 & 0 \0 & s_y & 0 & 0 \0 & 0 & s_z & 0 \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}2 & 0 & 0 & 0 \0 & 2 & 0 & 0 \0 & 0 & 2 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{scale}^{-1}=\left[\begin{matrix}0.5 & 0 & 0 & 0 \0 & 0.5 & 0 & 0 \0 & 0 & 0.5 & 0 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$M_{w→v}=M_{s}^{-1}M_{r}^{-1}M_{t}^{-1}=\left[\begin{matrix}0.5 & 0 & 0 & 0 \0 & 0.5 & 0 & 0 \0 & 0 & 0.5 & 0 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}1 & 0 & 0 & 0\0 & 0 & 1 & 0 \0 & -1 & 0 & 0 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}1 & 0 & 0 & -4 \0 & 1 & 0 & -5 \0 & 0 & 1 & -6 \0 & 0 & 0 & 1\end{matrix}\right]=\left[\begin{matrix}0.5 & 0 & 0 & -2 \0 & 0 & 0.5 & -3 \0 & -0.5 & 0 & 2.5 \0 & 0 & 0 & 1\end{matrix}\right]$$
$$p_{view}=M_{w→v}×p_{world}=\left[\begin{matrix}0.5 & 0 & 0 & -2 \0 & 0 & 0.5 & -3 \0 & -0.5 & 0 & 2.5 \0 & 0 & 0 & 1\end{matrix}\right]\left[\begin{matrix}1\2 \3 \1\end{matrix}\right]=\left[\begin{matrix}-1.5\-1.5 \1.5 \1\end{matrix}\right]$$
坐标z需要取反。即真正的坐标是
$$p_{view}=\left[\begin{matrix}-1.5\-1.5 \-1.5 \1\end{matrix}\right]$$